
 |
Using the many analytical techniques above will help to
determine how the part in question actually failed, what the mode of failure was
and where the failure was initiated. What is missing is a quantitative idea of
the stress environment in the failure and the response of the failed part to
that stress. The relatively new science of fracture mechanics can provide a
quantitative framework within which the failure may be understood. Fracture mechanics relates the size of flaws in a material,
principally cracks, to the applied stresses on those cracks and to the “fracture
toughness” of the material, or its resistance to cracking.
Fractures include both initiation and growth phases. After initiation, perhaps at a pit or some other site of stress-concentration, the crack will only grow when the stresses at the crack tip exceed a critical value known as the “fracture toughness” or KIc. If KIc and the stress conditions are known for a given material, then it is possible to calculate the size of crack that can be tolerated in that material without having the crack grow further. The following equation shows those conditions. A crack will propagate if:
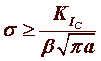
where σ (sigma) is the fracture stress, β (beta) is a dimensionless shape factor and a is the crack length for a crack with only one tip (i.e. not an internal crack, but one opening at a surface). Handbooks for engineering calculations have tables of values for Beta for different geometries. If the fracture toughness of the material is known, the fracture stress or critical crack size of a component can be calculated if the stress intensity factor is known. This calculation will allow:
the determination of “permissible flaw size,”
the calculation of the stress necessary to cause catastrophic failure
the determination of the load on a component at the time of failure
the determination as to whether adequate materials were used in manufacturing
the determination as to whether a part design was adequate
If the system that failed is well documented, then operational stresses can be calculated. For example, it can be determined how great the load was on a certain part when it failed. The load history may also be known throughout the time that the part was used. These data can be used to calculate the toughness, given a knowledge of the crack size at the time of final failure. This will show whether the part performed according to the specifications for it.
On the other hand, if the stresses are not known, then toughness still can be estimated from materials handbooks, again knowing the crack size and the area of the remaining sound metal at the time of failure. If neither toughness nor stresses are known, toughness can be estimated from physical testing, using Charpy-impact tests on pieces of the material. The stresses at failure can be determined by back-calculation and it can then be said if the part failed from overload.
Much can be also done to quantify conditions from fatigue failures. The rate of crack-growth can be estimated from a knowledge of the number of striations per unit length of crack perpendicular to the crack front. If the stresses are known, the stress intensity can be inferred, and the adequacy of the material for the use conditions can be determined. From a knowledge of the known stresses, the crack size at fracture and the crack growth-rate, estimates may be made as to whether or not the material had been misused. Thus, fracture mechanics can be used to help us understand:
how a particular crack formed at a specific location, and
the stress conditions that caused the crack to propagate
The design engineer will normally include “factors of safety” in his design to prevent stresses from reaching critical levels .
See: Pipeline example