Table 2 Pitting corrosion Fatigue Models

• Hoeppner(1971 - current)

• Lindley et al. (1982)

• Kawai and Kasai(1985)

• Kondo(1989)

Hoeppner(1971 - current)

• Summary

  • Proposed a model to determine critical pit depth to nucleate a Mode I crack under pitting corrosion fatigue conditions.

  • combined with the pit growth rate theory as well as the fatigue crack growth curve fit in a corrosive environment, the cycles needed to develop a critical pit size that will form a Mode I fatigue crack can be estimated.

• Description

  • Using a four parameter Weibull fit, fatigue crack growth threshold (DK_th) was found from corrosion fatigue experiments for the particular environment, material, frequency, and load spectrum.

  • The stress intensity relation for surface discontinuity (half penny shaped crack) was used to simulate hemispherical pit (Equation 2).

  • Using the threshold determined empirically, critical pit depth was found from the stress intensity relation mentioned above.

  • Then, the time to attain the pit depth for the corresponding threshold value was found using

    

    where, t is the time, d is the pit depth, and c is a material/environment parameter.

• Advantages/Limitations

  • This model provides a reasonable estimate for hemispherical geometry of the pits.

  • This model is useful to estimate the total corrosion fatigue life with knowledge of the kinetics of pitting corrosion and fatigue crack growth.

  • This model did not attempt to propose mechanisms of crack nucleation from corrosion pits.

  • This model is valid only for the conditions in which LEFM concepts are applicable.

  • Material dependent.

(back to top)

Lindley et al. (1982)

• Summary

  • Similar to Hoeppner's model, a method for determining the threshold at which fatigue cracks would grow from the pits was proposed.

• Description

  • Pits were considered as semi-elliptical shaped sharp cracks

  • Used Irwin's stress intensity solution for an elliptical crack in an infinite plate and came up with the relationship to estimate threshold stress intensity values related to fatigue crack nucleation at corrosion pits.

    

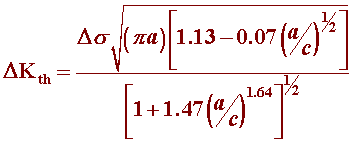
    where, Ds is the stress range, a is the minor axis, and c is the major axis of a semi-elliptical crack.

  • From the observed pit geometry i.e. for a/c ratio, threshold stress intensity can be calculated.

  • For the corresponding a/c ratio, critical pit depth can be estimated.

• Advantages/Limitations

  • The proposed stress intensity relation can be used in tension - tension loading situations where stress intensity for pits and cracks are similar.

  • Critical pit depths for cracked specimens can be estimated using the existing threshold stress intensity values.

  • This model is valid only for the conditions in which LEFM concepts are applicable.

  • Material dependent

(back to top)

Kawai and Kasai(1985)

• Summary

  • Proposed a model based on estimation of allowable stresses under corrosion fatigue conditions with emphasis on pitting.

  • As corrosion is not usually considered in developing S-N fatigue curves, a model for allowable stress intensity threshold involving corrosion fatigue conditions was proposed..

• Description

  • Considered corrosion pit as an elliptical crack.

  • Based on experimental data generated on stainless steel, new allowable stresses based on allowable stress intensity threshold was proposed

    

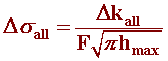
    where, DK_all can be determined from a da/dN vs. DK plot for a material, h_max is the maximum pit depth, and F is a geometric factor.

• Advantages/Limitations

  • Using this model, allowable stress in relation to corrosion fatigue threshold as a function of time can be estimated.

  • Material dependent.

  • This model is valid only for the conditions in which LEFM concepts are applicable..

(back to top)

Kondo(1989)

• Summary

  • Corrosion fatigue life of a material could be determined by estimating the critical pit condition using stress intensity factor relation as well as the pit growth rate relation.

• Description

  • Pit diameter was measured intermittently during corrosion fatigue tests.

  • From test results, corrosion pit growth law was expressed as

    

    where, 2c is the pit diameter, t is the time, and C_p is an environment/material parameter. Then, critical pit condition (DK_p) in terms of stress intensity factor was proposed by assuming pit as a crack:

    

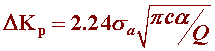
    where, s_a is the stress amplitude, a is the aspect ratio, and Q is the shape factor.

  • Critical pit condition was determined by the relationship between the pit growth rate theory and fatigue crack growth rates:

    

    where, N is the number of stress cycles, f is the frequency, and 2c is the pit diameter.

  • The pit growth rate dc/dN was developed using DK relation as given below:

    

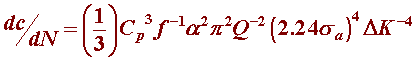
    dc/dN was determined using experimental parameter C_p.

  • Finally, the critical pit size 2C_cr was calculated from the stress intensity factor relation:

    

• Advantages/Limitations

  • The aspect ratio was assumed as constant.

  • Material and environment dependent.

(back to top)

Review of Pitting Corrosion Fatigue Models, D.W. Hoeppner, V. Chandrasekaran, and A.M.H. Taylor, University of Utah and FASIDE International Inc.