
 |
The following figure illustrates how a typical lead-acid battery behaves at different discharge currents. In this example, the battery capacity in Ah, is specified at the 20 hour rate, i.e. for a steady discharge (constant current) lasting 20 hours. The discharge current, in amps (A), is expressed as a fraction of the numerical value of C.
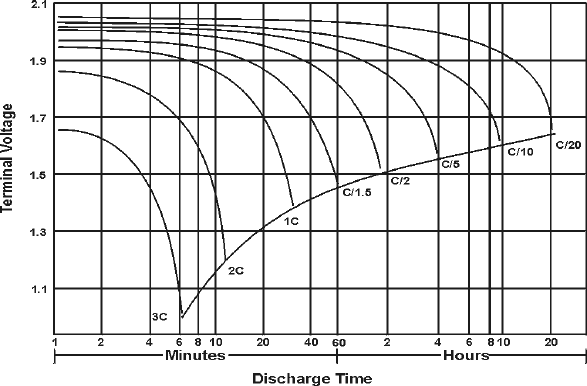
Typical tubular positive lead-acid cell behavior at various discharge currents.
For example, 0.2 C means C/5 A, and discharging will take approximately 5 hours. If C = 40 Ah, a current of 4 A can be expressed as 0.1 C. This is a way of normalizing characteristics so that batteries of different sizes can be described by a single set of graphs. Since a battery may be rated, i.e. its performance specified, for different discharge times, its rated capacity should normally indicate the current used.
The discharge current may alternatively be expressed as a multiple of the rated discharge current. For example, if the battery is specified at the 10 hour rate, I10 = C/10 (Ah/h) and is the current which would discharge the battery in 10 hours. Then, if C = 40 Ah, I10 = 40/10 = 4 A and a current of 10 A can be written as 2.5 I10.
It is convenient to talk about constant current loads, but it must be remembered that real applications of portable batteries usually involve a constant resistive load. In this case, the current is related to the voltage in relation to Ohm's law. Many systems , such as nickel-cadmium, lead-acid, and lithium-sulfur di, have a fairly constant voltage during discharge meaning that under a purely resistive load, the current is still fairly constant.
At increased discharge currents there is a decline in the quantity of charge that can be extracted before the voltage drops to the minimum acceptable value, as indicated by the dotted line in the previous figure. For example, at a current of 3C, this stage is reached in just over 6 min or 0.1 hour and the extractable capacity is only [3C (A) x 0.1 (h)], i.e. 0.3 C or 30% of the nominal capacity.
Note that the average voltage at a discharge current of 3C has fallen to approximately 80% of the voltage obtained at much lower currents. This reduces even further the energy, which can be extracted at increased lower levels. A smaller "end-voltage" is also permissible at high discharge currents because of internal voltage drops, which will disappear when the current is turned off. The "lost" capacity at high rates is still present in the cell and some further capacity can be extracted after resting at open circuit. A good example of such recovery are car batteries on cold days.