Module Four of CCE 281 Corrosion: Impact, Principles, and Practical Solutions

Free Energy of a Corrosion Reaction

In electrical and electrochemical processes, electrical work is defined as the product of charges moved (Q) times the potential (E) through which it is moved. If this work is done in an electrochemical cell in which the potential difference between its two half-cells is E, and the charge is that of one mole of reaction in which n moles of electrons are transferred, then the electrical work (-w) done by the cell must be nE. In this relationship, the Faraday constant F is required to obtain coulombs from moles of electrons. In an electrochemical cell at equilibrium, no current flows and the energy change occurring in a reaction is expressed in equation: (reference)

Under standard conditions, the standard free energy of the cell reaction DG⁰ is directly related to the standard potential difference across the cell, E⁰:

For solid or liquid compounds or elements, standard conditions are the pure compound or element; for gases they are 100 kPa pressure; and for solutes they are the ideal 1 molar (mol/L) concentration.

Electrode potentials can be combined algebraically to give cell potential. For a galvanic cell, such as the Daniell cell, a positive cell voltage will be obtained if the difference is taken in the usual way, as equation.

The free energy change in a galvanic cell, or in a spontaneous cell reaction, is negative and the cell voltage positive. The opposite is true in an electrolytic cell that requires the application of an external potential to drive the electrolysis reaction, in which case E_cell would be negative.

Other thermodynamic quantities can be derived from electrochemical measurements. For example, the entropy change (DS) in a cell reaction is given by the temperature dependence of DG:

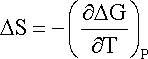
hence

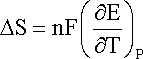
and

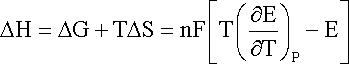
where DH is the enthalpy change and T the absolute temperature (K).

The equilibrium constant (K_eq) for the same reaction can be obtained with the following equation: