
 |
In this section, two of the PCF models proposed in the past viz. Hoeppner [41], and Kawai & Kasai [48] are examined to illustrate the applicability of these models in practice. Hoeppner in 1979 proposed the first model to estimate the time or cycles for a pit to reach the critical pit depth to nucleate a Mode I crack under pitting corrosion fatigue conditions based on the conceptual framework presented in 1971. It was proposed that with the pit growth rate theory as well as data from fatigue crack growth experiments in a corrosive environment, the cycles needed to develop a critical pit size that will form a Mode I fatigue crack can be estimated.
Using this model, the pit-to-crack transition length and cycles to failure for various stresses can be determined. However, currently, there are many unknowns for the analysis of an aircraft component to estimate accurately the fatigue life under PCF conditions. For example, for any material, no attempt has been made to date to determine the rate of pitting growth and the size of pits at various times. This is necessary to determine the Phase 1 life (L1, time or cycles to nucleate pits) of a component under PCF conditions. Once the pits are formed, it is necessary to estimate the time or cycles for the pits to reach a critical condition or critical depth to nucleate fatigue cracks from those pits (L2). First, the transition of pits to "short" cracks occur and then cracks will grow to "long" cracks [50]. Therefore, the time or cycles to form "short" cracks from fatigue nucleated pits and propagation to mode I crack need to be determined to estimate the Phase 2 life (L2) of a component. To accurately estimate the PCF life of a component using the model proposed by Hoeppner, the following information is necessary to estimate the Phase 1 and the Phase 2 of the total fatigue life.
As mentioned in Table 2, Kawai and Kasai proposed a model to estimate allowable stresses based on the allowable stress intensity threshold. They recognized that large safety factors are often used in determining allowable stresses because considerations like corrosion are often neglected in S-N curves. Knowing the allowable stress intensity threshold (Kall) determined from corrosion fatigue experiments and the maximum pit depth (hmax) measured from corrosion pit growth rate experiments for a given "machine-material-environment system", the allowable stress at which the particular component can be operated is determined using the following relation (Equation 1):
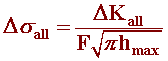
where, DKall can be determined from a da/dN vs. DK plot for a material, hmax is the maximum pit depth, and F is a geometric factor.
Combining these two models, two approaches are suggested to estimate the total fatigue life of a component under PCF conditions as discussed below.
First approach: The first approach needs data from either failure analysis or extensive experimentation on the design problem of interest. Both approaches are vital. Assuming that the failure analysis of a component revealed that the fatigue crack originated from a pit and because of it fracture occurred, then, the depth of the pit (a) could be measured. The quantified pit depth can be correlated to the pit growth rate curve for the material and the time or cycles to nucleate the size of the pit measured from failure analysis can be determined (Phase 1, L1). From this, an estimate of the stress value for pit-to-crack transition corresponding to the measured pit depth (from fracture analysis) can be made. The critical crack size for instability (ac) can be calculated for the given value of KIC for the material as well as the maximum applied stress for the component. Then, 'a' can be used in the calculation as the initial crack size and knowing the stress intensity threshold value, as well as ac, the total number of cycles to failure can be estimated using the Paris relation as explained in the later part of this section.
Second approach: The second approach involves determining the pit-to-crack transition length under various stresses using the stress intensity threshold value from fatigue crack growth experiment as explained in the following steps:
Review of Pitting Corrosion Fatigue Models, D.W. Hoeppner, V. Chandrasekaran, and A.M.H. Taylor, University of Utah and FASIDE International Inc.