
 |
The term activation
polarization makes reference to retarding factors that are an inherent part of the
kinetics of all electrochemical reactions. For example, consider the evolution of
hydrogen gas illustrated previously for
zinc
in air-free hydrochloric acid:
![]()
While this
reaction seems to be relatively simple, the rate at which hydrogen ions are
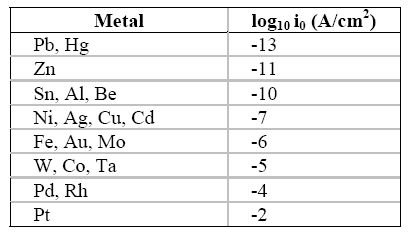
The exchange current density (i0) is surely the single most important variable that explains the large differences in the rate of hydrogen on metallic surfaces. Table 5.1 contains the approximate exchange current density for the reduction of hydrogen ions on a range of materials.
Approximate exchange current density (i0) for the hydrogen oxidation reaction on different metals at 25oC
Note that
the value for the exchange current density of hydrogen evolution on platinum is
approximately 10-2
A/cm2 whereas on mercury and lead it is
10-13
A/cm2, eleven orders of magnitude for the rate of this
particular reaction, or one hundred billion times easier on platinum than on mercury
or lead!
Propose an alloy modification that would possibly disfavor the production of hydrogen at an electrode. ... and one that would favor it.
This is the reason why mercury is often added to power cells such
as the popular alkaline primary cells to stifle the thermodynamically favored production
of gaseous hydrogen and prevent unpleasant incidents. This is also why lead acid
batteries (car batteries) can provide power in a highly acidic environment in a
relatively safe manner.
However, there is no simple method to estimate the exchange current density for a specific system. The exchange current density must be determined experimentally by scanning the potential with a laboratory set-up such as shown in Figure 5.1. In this experimental arrangement a potenstiostat/galvanostat power controller is used to pass current through the sample, or working electrode (W), and an auxiliary electrode (AUX) immersed in solution while monitoring the potential of the working electrode with a reference electrode and a Luggin capillary.
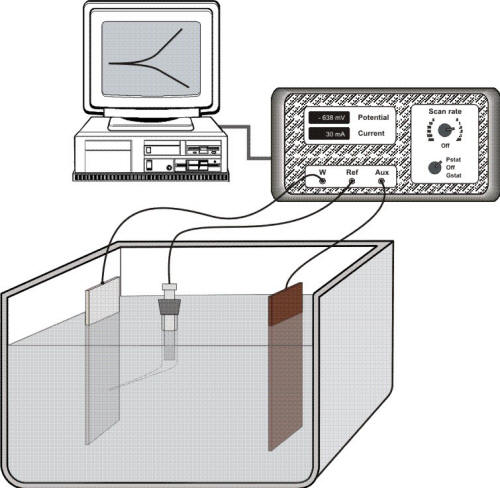
Electrochemical instrumentation to carry out potentiodynamic measurements in which a potenstiostat/galvanostat power controller is used to pass current through the sample, or working electrode (W), and an auxiliary electrode (AUX) while monitoring the potential of the working electrode with a reference electrode
The following theory explains
the basic mathematics that may then be used to extract exchange current density
from the results obtained. A general representation of the polarization of an electrode
supporting one specific reaction is given in the Butler-Volmer
equation:
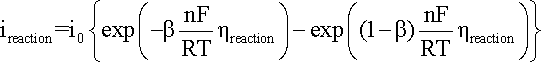
where:
ireaction
is the anodic or cathodic current;
b is the charge transfer barrier (symmetry coefficient) for the anodic or cathodic reaction, usually close to 0.5
n is the number of participating electrons
R is the gas constant, i.e. 8.314 J mol-1 K-1
T is the absolute temperature (K)
F corresponds to 96,485 C/(mole of electrons)
The exchange current density is a fundamental characteristic that can be defined as the rate of oxidation or reduction of the electrode at equilibrium expressed in terms of current. The presence of two polarization branches in a single reaction expressed in equation is illustrated in the following Figure for the polarization of a palladium electrode immersed in a solution containing similar concentrations of ferric (Fe3+) and ferrous (Fe2+) ions with a completely reversible reaction :
![]()
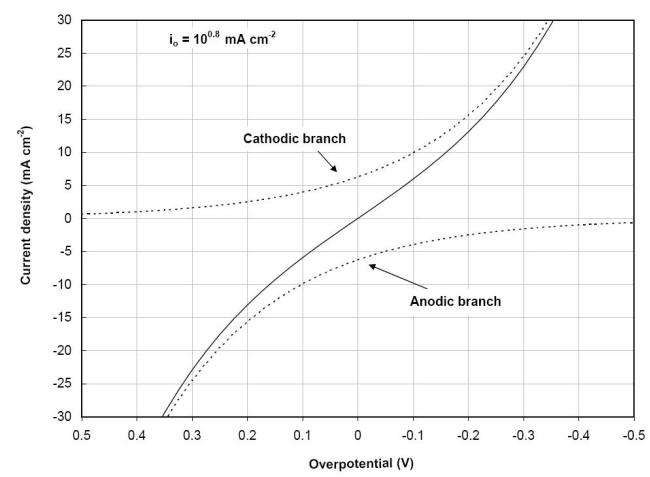
Current vs.
overpotential polarization plot of the
ferric/ferrous ion reaction on palladium showing both the anodic
and cathodic branches of the resultant current behavior
When
hreaction
is cathodic, i.e. negative, the second term in the
Butler-Volmer equation becomes negligible and the cathodic
current density (ic) can
be expressed by a simpler equation and
its logarithm:


where
bc is the cathodic
Tafel coefficient described in equation
that can be obtained from the slope
of a plot of
h against
log |i|, with the intercept yielding
a value for i0 as shown
in the following Figure.
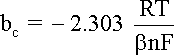
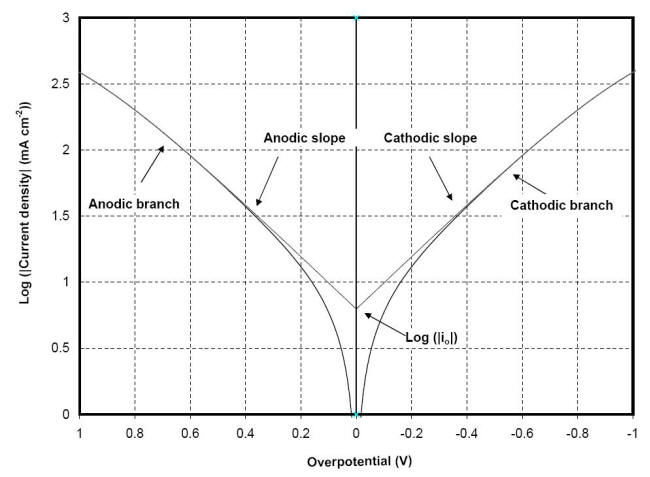
E of a plot of h against log |i| or Tafel plot showing the exchange current density can be obtained with the intercept
Similarly, when
hreaction
is anodic, i.e. positive, the first term in the Butler-Volmer
equation becomes negligible and the anodic current density (ia)
can be expressed by equation and its logarithm, with
ba obtained by plotting
hreaction
vs. log |i|:
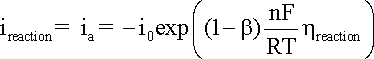
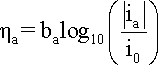
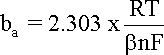
| (previous) | Page 3 of 10 | (next) |