Module Eight of CCE 281 Corrosion: Impact, Principles, and Practical Solutions

Scaling Indices

Encrustation of tubing, boilers, coils, jets, sprinklers, cooling towers, and heat exchangers arise wherever hard water is used. Scale formation can greatly affect heat transfer performance. One mm thick scale, for example, can add 7.5% to energy costs, while 1.5 mm adds 15% and 7 mm can increase cost by over 70%. Many factors can affect scaling. Scaling, which is basically the deposition of mineral solids on the interior surfaces of water lines and containers, most often occurs when water containing the carbonates or bicarbonates of calcium and magnesium is heated.

The saturation level (SL) of water in a mineral phase is a good indicator of the potential for scaling due to that specific scalant. SL is a ratio between the ion activity product (IAP) and the thermodynamic solubility product (Ksp) of a specific compound in that water. For example, when calcium carbonate (CaCO₃) is the scalant SL is defined as:

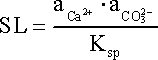
where is the IAP of the two ions involved in the formation of CaCO₃, i.e. Ca²⁺ and CO₃^2-.

K_sp is a measure of ionic concentration when dissolved ions and undissolved ions are in equilibrium. When a saturated solution of sparingly or slightly soluble salt is in contact with undissolved salt, equilibrium is established between the dissolved ions and the undissolved salt. In theory, this equilibrium condition is based upon an undisturbed water maintained at constant temperature and allowed to remain undisturbed for an infinite period of time.

In this example, water is said to be undersaturated (SL value less than 1) if it can still dissolve calcium carbonate. When water is at equilibrium, SL will be 1.0 by definition. Supersaturated water (SL value greater than 1) will precipitate calcium carbonate from water if allowed to rest. As the saturation level increases beyond 1.0, the driving force for the precipitation of calcium carbonate increases.

The following sections will describe some indices that have gained wide acceptance in the corrosion community. However, it should be stated that these indices are designed to indicate the tendency of given waters to deposit scales on metal substrates and surely not to predict the absolute corrosivity of specific waters. Generally speaking, scales precipitated onto metal surfaces can provide protection of the substrate from general corrosion. If on the other hand the scales are defective and contain voids and/or cracks. they could lead to localized corrosion. The assumption that water below saturation with respect to calcium carbonate is corrosive, while occasionally correct, is not reliable.

Langelier Saturation Index (LSI)

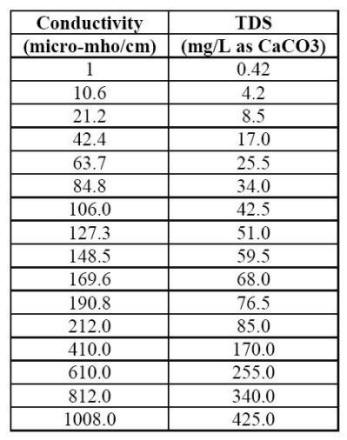
The LSI is probably the most widely used indicator of cooling water scale potential. This index indicates the driving force for scale formation and growth in terms of pH as a master variable. In order to calculate the LSI, it is necessary to know the alkalinity (mg L^-1 as CaCO₃ or calcite), the calcium hardness (mg L^-1 Ca²⁺ as CaCO₃), the total dissolved solids (mg L^-1 TDS), the actual pH, and the temperature of the water (^oC). If TDS is unknown, but conductivity is, one can estimate mg L^-1 TDS using the following conversion Table.

Conversion table between the conductivity of natural water and the total dissolved solids (TDS) it contains.

LSI is defined as:

Where: pH is the measured water pH

pHs is the pH at saturation in calcite or calcium carbonate and is defined as:

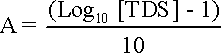
As for the SL reasoning described earlier, the LSI indicates three situations:

• If LSI is negative: No potential to scale, the water will dissolve CaCO3

• If LSI is positive: Scale can form and CaCO3 precipitation may occur

• If LSI is close to zero: Borderline scale potential

Water quality or changes in temperature, or evaporation could change the index.

As an example, suppose the drinking water supplied to animals has the following analysis:

pH = 7.5

TDS = 320 mg/L

Calcium = 150 mg L-1 (or ppm) as CaCO₃

Alkalinity = 34 mg L-1 (or ppm) as CaCO₃

The LSI index is calculated at two temperatures, i.e. 25^oC (room temperature) and 82^oC (cage wash cycle). The colder incoming water will warm to room temperature in the manifolds. Residual water in the rack manifold can be heated to 82^oC when the rack is in the cage washer.

LSI Formula:

LSI = pH - pH_s

pH_s = (9.3 + A + B) - (C + D) where: A = (Log₁₀[TDS] - 1)/10 = 0.15

B = -13.12 x Log₁₀(^oC + 273) + 34.55 = 2.09 at 25°C and 1.09 at 82°C

C = Log₁₀[Ca²⁺ as CaCO₃] - 0.4 = 1.78

D = Log₁₀[alkalinity as CaCO₃] = 1.53

Calculation at 25^oC:

pH_s = (9.3 + 0.15 + 2.09) - (1.78 + 1.53) = 8.2

LSI = 7.5 - 8.2 = - 0.7

Hence No Tendency to Scale

Calculation at 82^oC:

pH_s = (9.3 + 0.15 + 1.09) - (1.78 + 1.53) = 7.2

LSI = 7.5 - 7.2 = + 0.3

Hence Slight Tendency to Scale

Ryznar Stability Index (RSI)

The Ryznar stability index (RSI) uses a correlation established between an empirical database of scale thickness observed in municipal water systems and associated water chemistry data. Like the LSI, the RSI has its basis in the concept of saturation level. The Ryznar index takes the form:

RSI = 2(pHs) - pH

The empirical correlation of the Ryznar stability index can be summarized as follows:

RSI < 6 the scale tendency increases as the index decreases

RSI > 7 the calcium carbonate formation probably does not lead to a protective corrosion inhibitor film

RSI > 8 mild steel corrosion becomes an increasing problem.

Puckorius Scaling Index (PSI)

The PSI is based on the buffering capacity of the water, and the maximum quantity of precipitate that can form in bringing water to equilibrium. Water high in calcium, but low in alkalinity and buffering capacity can have a high calcite saturation level. The high calcium level increases the ion activity product. Such water might have a high tendency to form scale due to the driving force, but scale formed might be of such a small quantity as to be unobservable. The water has the driving force but not the capacity and ability to maintain pH as precipitate matter forms.

The PSI index is calculated in a manner similar to the Ryznar stability index. Puckorius uses an equilibrium pH rather than the actual system pH to account for the buffering effects:

PSI = 2 (pH_s) - pH_eq

Where:

pH_s is still the pH at saturation in calcite or calcium carbonate

pH_eq = 1.465 x log₁₀[Alkalinity] + 4.54

[Alkalinity] = [HCO₃^-] + 2 [CO₃^2-] + [OH^-]

Larson-Skold Index

The Larson-Skold index is based upon evaluation of in-situ corrosion of mild steel lines transporting Great Lakes waters. The index is the ratio of equivalents per million (epm) of sulfate (SO42-) and chloride (Cl-) to the epm of alkalinity in the form bicarbonate plus carbonate:

Extrapolation to other waters than the Great Lakes, such as those of low alkalinity or extreme alkalinity, goes beyond the range of the original data. The index has proven a useful tool in predicting the aggressiveness of once through cooling waters. The Larson-Skold index might be interpreted by the following guidelines:

Index < 0.8 chlorides and sulfate probably will not interfere with natural film formation

0.8 < index < 1.2 chlorides and sulfates may interfere with natural film formation. Higher than desired corrosion rates might be anticipated

Index > 1.2 the tendency towards high corrosion rates of a local type should be expected as the index increases

Oddo-Tomson Index

The Oddo-Tomson index accounts for the impact of pressure and partial pressure of carbon dioxide on the pH of water, and on the solubility of calcium carbonate. This empirical model also incorporates corrections for the presence of two or three phases (water, gas, and oil). Interpretation of the index is by the same scale as for the LSI and Stiff-Davis indices.