Boundary Element Modeling

Early predictions of corrosion rates and estimates of adequate cathodic protection (CP) have traditionally been based on case studies and sample exposure tests. Applying these techniques to real structures usually involve extrapolations, use of large safety factors and ongoing corrections and maintenance of the system. In the late 1960’s the finite element method was applied to the problem by discretization of the electrolytically conductive environment with a mesh.

The mathematical solution is found at the intersection points, or nodes, of the mesh. The solution is numerical because an approximate form of Laplace equation governs variations of the solution between adjacent nodes. However, creating a finite element mesh can be an extremely tedious and time-consuming process and, even when the mesh generation process is automated, it is difficult to perform a simulation when there are large geometry scale differences in the model, which is exactly the case found in most corrosion control problems where anodes are small compared with the size of the structure and the problem areas are most likely in corners and areas of complex geometry. (reference)

In the late 1970’s, boundary element (BE) methods became available. As the name implies, this numerical method requires mesh elements to be created, but now only on the boundary (or surfaces) of the problem geometry.

The main advantages of boundary elements for impressed current cathodic protection (ICCP) analysis are:

• Meshes are now only on the surface, hence only two-dimensional elements are required. Mesh generators can be used with confidence, and models can be constructed extremely quickly and inexpensively once the geometry is defined;

• Models can be created with fine detail of key or complex areas while modeling the whole structure or large volume of electrolyte;

• BE methods are very effective and accurate for modeling large or infinite domains as is the case for CP analysis.

The design goal of an ICCP system is to produce an evenly distributed protection potential on the structure as well as to reduce the power consumption of the anodes to a minimum. The available design variables are the number of anodes, their location, and the location of the reference cells.

The constraints on the design are the values of the potential on the structure. In order to provide adequate protection the potential must be less than a specified value, e.g. -800mV. In order to prevent overprotection the potential must be greater than a specified value, e.g. -900mV. By combining an automatic optimization procedure with the BE model of the ICCP system an optimum solution can be obtained. The equation governing electrochemical corrosion for the wetted surface of a ship hull is:

where F is the potential and k is the conductivity of the electrolyte.

This equation is valid if the electrolyte is homogeneous, there are no electrical sources or sinks, and the system is electroneutral.A shipboard ICCP system can be modeled in such a way to meet these conditions. Seawater is often represented as a uniform mixture of multiple components.Current source points and exposed metal can be represented by boundary conditions eliminating the need to include sources and sinks in the model.

Electroneutrality maintains charge equilibrium for the ship, surrounding water and ICCP system. The solution space for problem defined by Equation 2 used in the boundary element approach is the surface G which bounds the domain W as defined by:

where G_A is the anodic surface, G_C is the cathodic surface and G_I is the insulated surface.

G must be continuous but all sections of one surface type do not have to be contiguous. An ICCP system consists of the surfaces to be protected, the anodes, the reference cells and the power supply. Anodes are defined by maintaining the potential at a constant value, F_A:

defining the current density as a constant, q_A, on a surface:

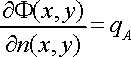
where F(x,y) is the electrical potential at the point (x, y) and n(x,y) is the normal to the surface at the point (x, y). Reference cells are defined as specific points on the hull where the mathematical solution is obtained.

It has been demonstrated that BE modeling can accurately predict experimental results.A major issue for accurate predictions is the availability of detailed polarization data. However, the lack of availability of accurate polarization data for a particular design condition does not eliminate all advantages associated with boundary element modeling. Reasonable polarization data can be used to obtain potential maps that identify good and bad regions of protection. BE methods also can be used to evaluate the effect of a single parameter on system performance. In this way basic understanding of electrochemical corrosion and parameter interactions can be obtained.Several parametric studies have been completed to date.

• Damage levels in the propeller area

• Seawater conductivity

• Finite paint resistance

• Influence of stray current source on system performance

On the object of stray current corrosion see also: DC traction, Cathodic protection, Coating, Contour plots, Definition, Detection, Examples, External currents, Historical perspective, Impressed current, Interference, Mechanisms, Modeling. Pipeline, Potential distribution, Prevention, Stray fields and leakage, Transit systems

See also: Boundary element modeling,Corrosion models, Knowledge based models, Mechanistic models, Pitting fatigue models, Risk based models